SCIENCE AND MATHEMATICS IN ANCIENT EGYPT

SCIENCE AND TECHNOLOGY IN ANCIENT EGYPT

Ancient Egyptian plane? The Egyptians developed fairly sophisticated chemistry through cosmetic-making, dying, glassmaking and gold metallurgy. The word chemistry is derived from the word Alchemy which is the ancient name for Egypt. In ancient times people, sciences such as chemistry, biology and physics did not exist. People believed that natural processes were caused by spirits. Even so, a great deal of practical knowledge was ascertained as properties of metals were observed and processes such as glassmaking and alloy production were figured out.

Pottery making was well advanced by 3000 B.C. The earliest Egyptian pottery was unglazed red earthenware. Both Mesopotamia and ancient Egypt had the pottery wheel by that time. The potter's wheel is believed to have been invented in Mesopotamia around 3500 B.C. and may be tied to the invention of wheeled vehicles. See Mesopotamia. Glassmaking was known in ancient Egypt as far back as 2500 B.C. The bottle was invented sometime around 1500 B.C. by Egyptian artisans. Glass from Egypt

The engineering skill of the ancient Egyptians has to be admired. Knowing only the lever, roller, inclined plane and possibly a long copper saw, they erected immense monuments in the desert, such as the Great Pyramid of Cheops, which stands 146 meters (481 ft. high) and contains 2 million limestone blocks, most weighing around 2.5 tons, and quarried several kilometers away and transported presumably on barges and sledges to their present location. [Source: Plumbing & Mechanical Magazine, July 1989, theplumber.com]

The Egyptians used primitive water wheels about 2500 B.C. built canals and irrigation systems. They didn’t make so many roads. Roads were not so important because they relied on the Nile for transportation. In 2300 B.C. the ancient Egyptians built channels through the first cataract of the Nile, where the Aswan Dan stands today. This helped open the way for trade between the Pharaohs and Africa. Messages were sent along the Nile. Seals were the equivalent of signatures. They were applied on wet mud with a paint-roller like cylinder.

Websites on Ancient Egypt: UCLA Encyclopedia of Egyptology, escholarship.org ; Internet Ancient History Sourcebook: Egypt sourcebooks.fordham.edu ; Discovering Egypt discoveringegypt.com; BBC History: Egyptians bbc.co.uk/history/ancient/egyptians ; Ancient History Encyclopedia on Egypt ancient.eu/egypt; Digital Egypt for Universities. Scholarly treatment with broad coverage and cross references (internal and external). Artifacts used extensively to illustrate topics. ucl.ac.uk/museums-static/digitalegypt ; British Museum: Ancient Egypt ancientegypt.co.uk; Egypt’s Golden Empire pbs.org/empires/egypt; Metropolitan Museum of Art www.metmuseum.org ; Oriental Institute Ancient Egypt (Egypt and Sudan) Projects ; Egyptian Antiquities at the Louvre in Paris louvre.fr/en/departments/egyptian-antiquities; KMT: A Modern Journal of Ancient Egypt kmtjournal.com; Ancient Egypt Magazine ancientegyptmagazine.co.uk; Egypt Exploration Society ees.ac.uk ; Amarna Project amarnaproject.com; Egyptian Study Society, Denver egyptianstudysociety.com; The Ancient Egypt Site ancient-egypt.org; Abzu: Guide to Resources for the Study of the Ancient Near East etana.org; Egyptology Resources fitzmuseum.cam.ac.uk

Time and Measurement in Ancient Egypt

The Egyptians invented the 24 hour day and helped pioneer the concept of time as an entity. They divided the day into two cycles of 12 hours each. The origin of the 12-hour division might come from star patterns in the sky or from the Sumerian number system which was based on the number 12.

According to the Guinness Book of Records, the oldest known measure is the beqa, used in ancient Egypt as far back as 3800 B.C. These cylindrical weights weighed 6.65 to 7.45 ounces. For measuring weight, the ancients used grains of wheat or barley corns; the grain to this day is one of the smallest units of weight, 1/7000 of a pound. The carat, used in weighing gems, was derived from the tiny carob seed. A deben was an ancient Egyptian measurement equal to three ounces.

The cubit, one the earliest forms of measurement known, was the distance between a person's elbow and fingertip — roughly 18 inches. The symbol for a cubit, a forearm, appeared on Egyptian papyrus texts thousands of years old. King Menes decreed a sacred or royal cubit 14 percent larger than the common cubit. This measurement was used to build his houses but was forbidden for others to use.

A cubit was the unit of measure throughout much of the ancient world. The measurement varied a great deal however. In ancient Egypt, for example, a cubit for a man was 17.72 inches while the cubit for a king was 20.62 inches. Both the Great Pyramids of Cheops and Noah's Ark were built to cubits. The latter was 300 cubits long.

Early Calendars

The Babylonians are often given credit for devising the first calendars, and with them the first conception of time an entity. They developed the used the 360-day year — divided into 12 lunar months of 30 days (real lunar months are 29½ days) — devised by the Sumerians and introduced the seven day week, corresponding to the four waning and waxing periods of the lunar cycle. The ancients Egyptians adopted the 12-month system to their calendar. The ancient Hindus, Chinese, and Egyptians, all used 365-day calendars.

The Babylonians stuck stubbornly to the lunar calendar to define the year even though 12 lunar months did not equal one year. In 432 B.C., the Greeks introduced the so-called Metonic cycle in which every 19 years seven of the years had thirteen months and 12 years had 12 months. These kept the seasons in synch with the year and the roughly kept the days and months of the Metonic year in synch with those on the lunar calendar. The Metonic calendar was too complicated for everyday use and used mostly by astronomers.

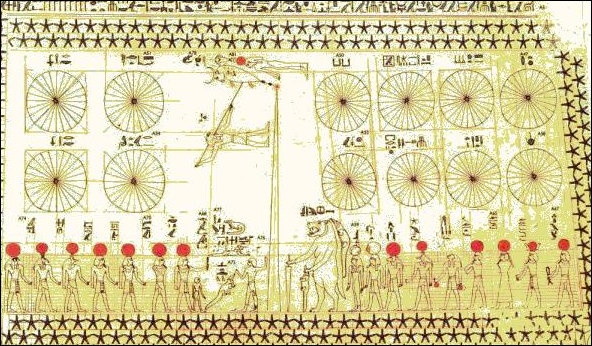
Calendar of Senenmut-Grab

The Mesopotamians also invented the 60 minute hour. The idea of measuring the year was more important than measuring the day. People could judge the time of day by following the sun. Judging the time of year was more difficult and important in knowing when to plant crops, expect rain or snow and harvest crops. That is why a yearly calendar was developed before clocks and minutes and seconds didn’t come to the Middle Ages.

The Babylonians have been credited with coming up with the idea of dividing the hour into 60 minutes. The number 60 seemed to be prized especially since 360 divided by six is 60 and some scholars have speculated that is why hours are made up of 60 minutes and minutes are made up of 60 seconds. Other believe the number 60 was arrived at by multiplying the visible planets (5, Mercury, Venus, Mars, Jupiter, and Saturn) by the number of months (12).

Ancient Egyptian Calendar

Although Mesopotamians devised the first calenders the Egyptians conceived the modern 365-day, 12 month calendar.

Egyptians added five days to the Babylonian 360-day calendar. The ancient Egyptian civil calendar had three season: 1) Akhet (Flooding); 2) Peret (Growing or Sowing); and 3) Shemu (Harvest). Each season had four months with 30 days. The additional five days were tacked onto the end of Harvest and set aside for feasting during the annual flooding of the Nile. The Hindus and Chinese also used 365-day calendars.

Egypt devised a 365-day calendar as early as the 5th millennium based on flood of the Nile which occurred at almost the same time every year. The Egyptian year began in July when the Nile usually flooded and was marked by the rising of the star Sirius in the eastern horizon just before daybreak.

The Egyptians discovered that not only did the star Sirius line up with the rising sun around the time of flooding every year they also noticed that Sirius lined up with sun about six hours (a ¼ a day) different every year. They were among the first people to realize the need for a leap day. For a while they inserted a leap day into their calendar but then abandoned it. This meant their calendar would slip a day every four years and an entire month every 120 years. A trilingual description of changes to be made to the Egyptian calendar was found at the temple of Bubastis, the 8th century capital of Egypt. The 2,200-year-old stellate described planned changes for the Egyptian calendar that were implemented d250 years later by Julius Caesar.

Ancient Egyptian Astronomy and Astrology

The Egyptians refined the Babylonian system of astrology and the Greeks shaped it into its modern form. Astrology as we know it originated in Babylon. It developed out of the belief that since the Gods in the heavens ruled man's fate, the stars could reveal fortunes and the notion that the motions of the stars and planets control the fate of people on earth. The motions of the stars and planets are mainly the result of the earth’s movement around the sun, which causes: 1) the sun to move eastward against the background of the constellations; 2) the planets and moon to shift around the sky; and 3) causes different constellations to rise from the horizon at sunset different times of the year.

night sky in the tomb of Seti I

In ancient times astrology and astronomy were the same thing. The Babylonians were the first people to apply myths to constellations and astrology and describe the 12 signs of the zodiac. The Greeks and Romans borrowed some of their myths from the Babylonians and invented their own. The word astrology (and astronomy) are derived from the Greek word for "star."

The names and shapes of many the constellations are believed to date to Sumerian times because the animals and figures chosen held a prominent place in their lives. It is thought that if the constellations originated with the the Egyptians were would ibises, jackals, crocodiles and hippos — animals in their environment — rather than goats and bulls. If they came from India why isn’t there a tiger or a monkey. To the Assyrians the constellation Capricorn was munaxa (the goat fish). The Greeks added names of heroes to the constellations. The Romans took these and gave them the Latin names we use today. Ptolemy listed 48 constellations. His list included ones in the southern hemisphere, which he and the Mesopotamians, Egyptians, Greeks and Romans couldn’t see.

Sara Moldaschel of Minnesota State University, Mankato wrote: “The Ancient Egyptians had a limited knowledge of astronomy. Part of the reason for this is that their geometry was limited, and did not allow for complicated mathematical computations. Evidence of Ancient Egyptian disinterest in astronomy is also evident in the number of constellations recognized by Ancient Egyptians. At 1100 B.C., Amenhope created a catalogue of the universe in which only five constellations are recognized. They also listed 36 groups of stars called decans. These decans allowed them to tell time at night because the decans will rise 40 minutes later each night. Theoretically, there were 18 decans, however, due to dusk and twilight only twelve were taken into account when reckoning time at night. Since winter is longer than summer the first and last decans were assigned longer hours. Tables to help make these computations have been found on the inside of coffin lids. The columns in the tables cover a year at ten day intervals. The decans are placed in the order in which they arise and in the next column, the second decan becomes the first and so on. [Sources: Sara Moldaschel Minnesota State University, Mankato, ethanholman.com, “The Cambridge Illustrated History of Astronomy.” Michael Hoskin, ed. Cambridge University Press,1997; Springer-Verlag and Hugh, Thurston. “Early Astronomy,” New York, Inc. 1994]

“Astronomy was also used in positioning the pyramids. They are aligned very accurately, the eastern and western sides run almost due north and the southern and northern sides run almost due west. The pyramids were probably originally aligned by finding north or south, and then using the midpoint as east or west. This is because it is possible to find north and south by watching stars rise and set. However, the possible processes are all long and complicated. So after north and south were found, the Egyptians could look for a star that rose either due East or due West and then use that as a starting point rather than the North South starting point. This would result in the pyramids being more accurately aligned with the East and West, which they are, and all of the errors in alignment would run clockwise, which they do. This is because of precession of the poles which is very difficult to view, and the Ancient Egyptians did not know about. This theory is further substantiated by the fact that the star B Scorpii’s rising-directions match with the alignment of the pyramids on the dates at which they were built. +\

“Ancient Egyptians also used astronomy in their calendars. There life revolved the annual flooding of the Nile. This resulted in three seasons, the flooding, the subsistence of the river, and harvesting. These seasons were divided into four lunar months. However, lunar months are not long enough to allow twelve to make a full year. This made the addition of a fifth month necessary. This was done by requiring the Sirius rise in the twelfth month because Sirius reappears around the time when the waters of the Nile flood. Whenever Sirius arose late in the twelfth month a thirteenth month was added. This calendar was fine for religious festivities, but when Egypt developed into a highly organized society, the calendar needed to be more precise. Someone realized that there are about 365 days in a year and proposed a calendar of twelve months with 30 days each, with five days added to the end of it. However, since a year is a few hours more than 365 days this new administrative calendar soon did not match the seasonal calendar.

sundial

Inventions by Ancient Egyptians

The Egyptians are credited with inventing writing, mathematics, geometry, surveying, metallurgy, astronomy, accounting, writing materials, medicine, the ramp, the lever, the plough, and mills for grinding grain. Whether they unilaterally were the first to devise these advancements is a matter of considerable debate but least they contributed greatly to their inception and widespread use. [Source: Mark Millmore, discoveringegypt.com discoveringegypt.com ^^^] Agriculture advancements credited to the ancient Egyptians include 1) the ox-drawn plough, 2) irrigation, 3) the sickle, a curved blade used for cutting and harvesting grain, and the shadoof, a long balancing pole with a weight on one end and a bucket on the other. The ox-drawn plough — - a plough pulled by oxten — revolutionized agriculture. Modern versions of the plough are still widely used today Egyptian irrigation consisted of canals and irrigation ditches primarily used to harness Nile river’s yearly flood and bring water to distant fields. The shadoof’s bucket could easily be filled with water and raised to bring water to higher ground. ^^^

The ancient Egyptians are also credited with toothpaste. Mark Millmore of discoveringegypt.com wrote: “At the 2003 dental conference in Vienna, dentists sampled a replication of ancient Egyptian toothpaste. Its ingredients included powdered of ox hooves, ashes, burnt eggshells and pumice. Another toothpaste recipe and a how-to-brush guide was written on a papyrus from the fourth century AD describes how to mix precise amounts of rock salt, mint, dried iris flower and grains of pepper, to form a “powder for white and perfect teeth.”“ [Source:Mark Millmore, discoveringegypt.com discoveringegypt.com ^^^]

Clocks in Ancient Egypt

Mark Millmore wrote in discoveringegypt.com: “In order to tell the time Egyptians invented two types of clock. Obelisks were used as sun clocks by noting how its shadow moved around its surface throughout the day. From the use of obelisks they identified the longest and shortest days of the year. An inscription in the tomb of the court official Amenemhet dating to the16th century B.C. shows a water clock made from a stone vessel with a tiny hole at the bottom which allowed water to dripped at a constant rate. The passage of hours could be measured from marks spaced at different levels. The priest at Karnak temple used a similar instrument at night to determine the correct hour to perform religious rites. [Source: Mark Millmore, discoveringegypt.com discoveringegypt.com ^^^]

Sarah Symons of McMaster University has pointed out that the idea that obelisks at temples as were used as sundials is probably untrue. Yes, there was connection between the obelisks and with the sun: the high point of an obelisk, covered with an alloy of gold and silver, reflected the sun before sunrise. The main function of obelisks, according to obelisk engravings, was to serve honor the pharaoh that commissioned it. Only when obelisks were taken from Egypt and placed in Rome and Paris were they used as a sundials.

Ancient Egyptian Sun Dials

20120217-sundial treppenuhr_Inv.jpg
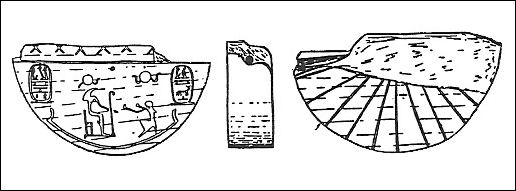
sundial The ancient Egyptians are thought to have been the first people to develop sun dials although there are some claims the Chinese developed them around the same time. The oldest Egyptian sun dials have been dated at 3500 B.C. A fragment of one at Metropolitan Museum of Art in New York has been dated to about 3000 B.C. The largest surviving sundial is the 31-meter-high obelisk of Karnak, erected around 1470 B.C. It casts its shadow on a temple of the sun god Amun Ra. A portable Egyptian sundial, or “shadow clock,” that survives from the time of Thutmose III (c. 1500 B.C.) is a horizontal bar about a foot long with a T-shaped structure at one end that casts a shadow on marks on the horizontal bar. In the morning the bar was set with the T facing east; at noon the T was revered and faced west. An example from the 8th century B.C. can be found at the Museum of the Ancient Agora in Athens.

Sun dials were of limited use in cloudy weather (which fortunately for Egyptians was rare) and at night. The sun' shadow moved so slowly it was relatively useless marking off minutes and seconds. Thutmose III era sundials were also useless early in the morning and late in the afternoon when the shadow was cast to an infinite length (this problem was later addressed by Greek sun dials, which were shaped like the interior of the bottom half of a globe).

The other problem with sundials is that they marked off hours that varied in length with the seasons (as the length of the day changed from short in the winter to long in the summer). Egypt is relatively near the equator so the days didn't change that much. Not until the 16th century were sundials marked with true hours, when people acquired pocket sundials as well as clocks.

The Egyptians used "temporary hours" or "temporal hours" which varied in length from day to day depending on what time the sun rose and set. The “Book of That Which Is” describes the 12 sections of the Underworld as each being related to an hour of the night.

Oldest Sundial and Its Use

20120217-sundial Cadran-portable-borchardt.jpg
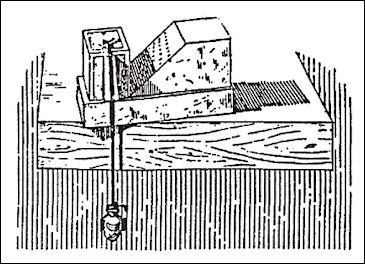
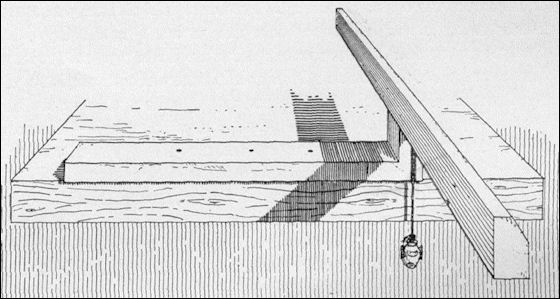
portable sundial One candidate for the oldest surviving sundial was found in Egypt and dates to around 1450 B.C. Located in the Egyptian museum in Berlin (catalog number 19744), and made of schist , it was probably found in Hermopolis in central Egypt and dates to the reign of Thutmosis III (1479 - 1425 B.C.) during the New Kingdom. The name and titles of the pharaoh are engraved on the side. [Source: http://www.wijzerweb.be/egypteengels.html]

The sundial is shaped like the letter L. The short piece is the gnomon (vertical rod giving a shadow). In the gnomon there is a hole for attaching a small plumb bob. Below is a vertical groove to align the thread of the plumb bob. In the horizontal plane of the long bar there are five circles — marks for the time scale. The distances between the marks are proportional to the numbers 1,2,3,4,5.

In 1910 the German Egyptologist Ludwig Borchardt hypothesized that the shadow of the gnomon gives an indication of the so-called unequal hours on the time scale. Because in the period between sunrise and sunset is shorter in winter than in summer, the hours are unequal depending on the season. Unequal hours were in use until the Middle Ages. The height of the sun also varies the seasons and this affects the length of the shadow. To give a shadow to the correct mark throughout the year, the gnomon should be variable in height. Therefore Borchardt assumed that the sundial, as it was found, is incomplete and needed a crossbar of a suitable height that served as an adjuster. He surmised these crossbars were lost. In 1965 the Dutch mathematician corroborated Borchardt’s hypothesi to some degree by calculating the shadow of a higher gnomon. He found that a reading from a certain mark was in agreement with reading at the other marks and was a good approximation of the measurement of the unequal hours.

In 1999 Sarah Symons of McMaster University in Ontario Canada defended her doctorate thesis "Ancient Egyptian Astronomy: Timekeeping and Cosmography in the New Kingdom," part of which rejected the theories of Borchardt and Bruins on L-shaped sundials using her knowledge of Egyptian texts and culture and the mathematical background of gnomonics. Symons refutes Borchardt’s theory on four arguments: 1) The sundial hieroglyph shows the L-shape with a small plumb bob, but no crossbar. 2) The calculation of the indications of unequal hours are not measured with a degree of accuracy that merits the addition of a crossbar. 3) Usage of the sundial: The only tool to set up the sundial, is the plumb bob to level it. Directing the sundial with the gnomon towards the sun - the shadow coinciding with the long part of the L-shape over its full width.

4) The text in the Osireon cenotaph name, near the temple of Seti I at Abydos, which describes the construction and usage of such L-shaped sundials. In the text and the accompanying drawing, there is nothing about a crossbar. The simple ratios of the distances between the marks are indicated as corresponding to 3, 6, 9, 12. As in other ancient Egypt drawings, the distances are not drawn to scale. The text describes these relations as "an established procedure.” A passage in the text on the orientation of the sundial can be interpreted in two ways: an east-west orientation with a rotation of 180 degrees at noon or a continuous turning towards the sun.

One of the World's Oldest Sundials Found in Valley of the Kings

ancient Egyptian sundial

In 2013, a team led by Prof. Susanne Bickel of the University of Basel announced that had found one of the world’s oldest sun dials in the Kings’ Valley. while clearing the entrance to one of the tombs. According to a University of Basel release: “The researchers found a flattened piece of limestone (so-called Ostracon) on which a semicircle in black color had been drawn. The semicircle is divided into twelve sections of about 15 degrees each. A dent in the middle of the approximately 16 centimeter long horizontal baseline served to insert a wooden or metal bolt that would cast a shadow to show the hours of the day. Small dots in the middle of each section were used for even more detailed time measuring. [Source: University of Basel, phys.org, March 15, 2013]

“The sun dial was found in an area of stone huts that were used in the 13th century BC to house the men working at the construction of the graves. The sun dial was possibly used to measure their work hours. However, the division of the sun path into hours also played a crucial role in the so-called netherworld guides that were drawn onto the walls of the royal tombs. These guides are illustrated texts that chronologically describe the nightly progression of the sun-god through the underworld. Thus, the sun dial could also have served to further visualize this phenomenon.” Bickel told Livescience: “"The significance of this piece is that it is roughly one thousand years older than what was generally accepted as time when this type of time measuring device was used...The piece was found with other ostraca on which small inscriptions, workmen's sketches, and the illustration of a deity were written or painted in black ink. One hypothesis would be to see this measuring device in parallel to the illustrated texts that were inscribed on the walls of the pharaohs' tombs and where the representation of the night and the journey of the sun god through the netherworld is divided into the individual hours of the night. The sundial might have been used to visualize the length of the hours." On the device being used to measure work hours, she said. "I wondered whether it could have served to regulate the workmen's working time, to set the break at a certain time, for example.” [Source: Jeanna Bryner, Live Science, March 20, 2013]

Ancient Egyptian Water Clocks

The ancient Egyptians developed water clocks (useful at night) in the 15th century B.C. Water clocks operate on the principle that water can be made to drip at a fairly constant rate from a bowl with a tiny hole in the bottom. To make sure that time scale remains constant water pressure had to remain constant and an effort had to be made to make sure that the hole in the vessel wasn't worn larger. The clocks were used primarily like hour glasses. Calibrating them to measure off uniform hours at night that were linked to the hours of the day, which changed depending on the season, was too complicated for the ancient Egyptians to deal with.

Daniel Boorstin wrote: the Egyptians had “both outflow and inflow models of water clocks. The outflow type was an alabaster vessel with a scale marked inside and a single hole near the bottom where the water dripped. By noting the drop of the water level inside from one mark to the next mark below on the scale, the passage of time was measured. The later inflow type, which marked the passing time by the rise of water in the vessel, was more complicated, as it required a constant source of regulated supply." [Source: Daniel Boorstin, "The Creators"]

Time was sometimes determined from lamps. Ancient lamp wicks were timed to last for four hours.

First Wheels, Wheeled Vehicles and Horses

Ancient Egyptian cart

The wheel, some scholars have theorized, was first used to make pottery and then was adapted for wagons and chariots. The potter’s wheel was invented in Mesopotamia in 4000 B.C. Some scholars have speculated that the wheel on carts were developed by placing a potters wheel on its side. Other say: first there were sleds, then rollers and finally wheels. Logs and other rollers were widely used in the ancient world to move heavy objects. It is believed that 6000-year-old megaliths that weighed many tons were moved by placing them on smooth logs and pulling them by teams of laborers.

Early wheeled vehicles were wagons and sleds with a wheel attached to each side. The wheel was most likely invented before around 3000 B.C.”the approximate age of the oldest wheel specimens — as most early wheels were probably shaped from wood, which rots, and there isn't any evidence of them today. The evidence we do have consists of impressions left behind in ancient tombs, images on pottery and ancient models of wheeled carts fashioned from pottery.◂

Evidence of wheeled vehicles appears from the mid 4th millennium B.C., near-simultaneously in Mesopotamia, the Northern Caucasus and Central Europe. The question of who invented the first wheeled vehicles is far from resolved. The earliest well-dated depiction of a wheeled vehicle — a wagon with four wheels and two axles — is on the Bronocice pot, clay pot dated to between 3500 and 3350 B.C. excavated in a Funnelbeaker culture settlement in southern Poland. Some sources say the oldest images of the wheel originate from the Mesopotamian city of Ur A bas-relief from the Sumerian city of Ur — dated to 2500 B.C. — shows four onagers (donkeylike animals) pulling a cart for a king. and were supposed to date sometime from 4000 BC. [Partly from Wikipedia]

In 2003 — at a site in the Ljubljana marshes, Slovenia, 20 kilometers southeast of Ljubljana — Slovenian scientists claimed they found the world’s oldest wheel and axle. Dated with radiocarbon method by experts in Vienna to be between 5,100 and 5,350 years old the found in the remains of a pile-dwelling settlement, the wheel has a radius of 70 centimeters and is five centimeters thick. It is made of ash and oak. Surprisingly technologically advanced, it was made of two ashen panels of the same tree. The axle, whose age could not be precisely established, is about as old as the wheel. It is 120 centimeters long and made of oak. [Source: Slovenia News]

The wheel and axle were found near a wooden canoe. Both the wheel and the axle had been scorched, probably to protect them against pests. Slovenian experts surmise that the wheel they found belonged to a single-axle cart. The aperture for the axle on the wheel is square, which means the wheel and the axle rotated together and, considering the rough ground, the cart probably had only one axle. We can only guess what the cart itself was like. The Ljubljana marshes are a perfect place for old objects to be preserved. There have been many finds uncovered in this area. Apart from the wooden wheel, axle and canoe, there have been innumerable objects found which are up to 6,500 years old.

A wheel dated to 3000 B.C., was found near Lake Van in eastern Turkey. Wheels with simialr dates have been found in germany and Switzerland. One very old wheel was a wooden disc discovered at an archeological sight near Zurich. The wheel now can be seen in the Zurich museum.

The invention of the wheel paved the way for more advanced technology such as pulleys, gears, cogs and screws. A flint point or stick spun with a bow was another important advancement. It could be used to make fire and employed as a drill.

Wheel on carts and potter’s wheels appeared around the same time, 4000 to 3500 B.C. (See First Villages). Some scholars have speculated that the wheels on carts was developed by placing a potters wheel on its side.

The Sumerians had no camels or horses. They did have sheep, goats and oxen which could be used as beasts of burden. Wheeled vehicles were used as carts. Most were pulled by oxen, onagers (donkeylike animals) or donkeys. A bas-relief from the Sumerian city of Ur (2500 B.C.) shows four onagers pulling a cart for a king.

Donkeys and onagers were the main beasts of burden. Goods were moved overland by donkey caravans. Donkeys and onagers later were replaced by horses who are less stubborn, faster, and have a lower threshold of pain (donkey's often do not move even when furiously whipped). The Assyrians and Egyptians used horses and chariots. The Hittites and the Hykos were the first people in the Middle East to use chariots. Chariots came before mounted riders.

Ancient Egyptian Metallurgy

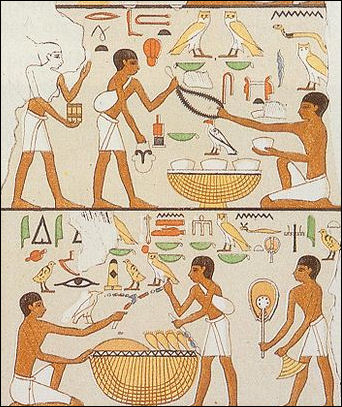
Early tools were made from copper and later bronze. Egyptian bronze tended to be around 88 percent copper and 12 percent tin. Iron was introduced by the Hittites in the 13th century but wasn't common until the 6th or 7th century B.C.

A wide variety of copper tools, fish hooks and needles were made. Chisels and knives lost their edge and shape quickly and had be reshaped with some regularity or simply thrown out. In the Old Kingdom (2700 to 2125 B.C.) there was only copper. Copper-making hearths have been found near the pyramids. Reliefs found nearby show Egyptians gathering around a fire smelting copper by blowing into long tubes with bulbous endings.

Knives tended be made from bronze. They were considerably sharper than copper knives. The sharpest knives of all were made of flaked obsidian. A wide variety of stone tools were also used, including pick axes and hammers.

Sculptures made of copper, bronze and other metals were cast using the lost wax method which worked as follows: 1) A form was made of wax molded around a pieces of clay. 2) The form was enclosed in a clay mold with pins used to stabilize the form. 3) The mold was fired in a kiln. The mold hardened into a ceramic and the wax burns and melted leaving behind a cavity in the shape of the original form. 4) Metal was poured into the cavity of the mold. The metal sculpture was removed by breaking the clay when it was sufficiently cool.

Egyptian alchemists thought that gold was a seed and the silver and copper were food that caused more gold to grow. One ancient Egyptian recipe for "diplosis" of gold called for two parts gold, one part copper and one part silver to be heated and mixed together. The result is twice as much gold (12 carat gold, when mixed the reddish tint of copper and the greenish tint of the silver doesn't change the color of the gold).

Mathematics in Ancient Egypt

The Egyptians used a base-10 system of numbers. Sometimes they used different symbols for 1s, 10s, 100s, 1,000s, 10,000s, 100,000s and 1,000,000s. Other times they used a group of hieroglyphic symbols for individual numbers. Egyptian arithmetic was based on a system binary system like that used to power computers today. Multiplication was done by duplicating numbers and adding the sums together. Division was the same operation performed backwards.

Peter Schjeldahl wrote in The New Yorker: “The Egyptians were perniciosus keepers of lists, and recorders of methods and procedures. They meant for things they made to last forever.”To rule effectively, the ancient Egyptians set up an efficient and extensive administration that levied taxes, conducted censuses, and maintained and supplied a large army — all of which required some mathematics. At first they used counting glyphs. By 2000 B.C., hieratic glyphs were in use.

Herodotus wrote: Ramses II “divided the land into lots and gave a square piece of equal size, from the produce of which he exacted an annual tax. [If] any man's holding was damaged by the encroachment of the river ... [The Pharoah] ... would send inspectors [and surveyors] to measure the extent of the loss, in order that he pay in future a fair proportion of the tax at which his property had been assessed. Perhaps this was the way in which geometry was invented, and passed afterwards in to Greece.

Building great monuments like the pyramids also took some mathematical knowledge, Democritus (~410 B.C.) wrote: No one surpasses me in the construction of lines with [the help of a ruler and compass], not even the so-called rope-stretchers (surveyors) among the Egyptians.” Jimmy Dunn of touregypt.net wrote: “Some of the pyramids indicate an accurate understanding of Pi, but the mathematical knowledge of the Egyptians did not include the ability to arrive at this by calculation. It is possible that this could have been arrived at "accidentally" through a means such as counting the revolutions of a drum.”

The Egyptians had a decimal system using seven different symbols. 1 is shown by a single stroke. 10 is shown by a drawing of a hobble for cattle. 100 is represented by a coil of rope. 1,000 a drawing of a lotus plant. 10,000 is represented by a finger. 100,000 a tadpole or frog. 1,000,000 figure of a god with arms raised above his head. The conventions for reading and writing numbers is quite simple; the higher number is always written in front of the lower number and where there is more than one row of numbers the reader should start at the top. [Source: Mark Millmore, discoveringegypt.com]

Ancient Egyptian Mathematical Papyri

The Rhind Mathematical Papyrus is one of the best known examples of Egyptian mathematics. Named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, it was apparently found during illegal excavations in or near the Ramesseum. Dated to around 1550 B.C., it contains 84 different calculations to help with various aspects of Egyptian life such as building a pyramid or determining the amount of grain needed to fatten a goose. [Source: Wikipedia +]

The Moscow Mathematical Papyrus is an ancient Egyptian mathematical papyrus, also called the Golenishchev Mathematical Papyrus. Dated to the 13th dynasty (1803- 1649 B.C.) and based on older material probably dating to the 12th dynasty, it is older but smaller than the Rhind Papyrus. The Moscow Papyrus is approximately 5½ m (18 ft) long and varies between 3.8 and 7.6 cm (1.5 and 3 in) wide.

The Moscow Mathematical Papyrus is divided into 25 problems with solutions. The problems are organized no particular order, and the solutions feature much less detail than those in the Rhind Papyrus. The Moscow papyrus is well known for its geometry problems. Problems 10 and 14 compute a surface area and the volume of a frustum respectively. The remaining problems deal with common subjects. Problems 2 and 3 are related to ship’s parts.Most of the problems are algebraic pefsu problems. A pefsu measures the strength of the beer made from a hekat of grain. +

Math in the Rhind Papyrus

The first part of the Rhind papyrus consists of reference tables and a collection of 21 arithmetic and 20 algebraic problems. The problems start out with simple fractional expressions, followed by completion (sekem) problems and more involved linear equations (aha problems).The second part of the Rhind papyrus, being problems 41-59, 59B and 60, consists of geometry problems. Problems 41 – 46 show how to find the volume of both cylindrical and rectangular granaries. Problem 47 is a table with fractional equalities which represent the ten situations where the physical volume quantity of "100 quadruple heqats" is divided by each of the multiples of ten, from ten through one hundred. [Source: Wikipedia]

Rhind mathematical papyrus

The third part of the Rhind papyrus consists of the remainder of the 91 problems, being 61, 61B, 62-82, 82B, 83-84, and "numbers" 85-87, which are items that are not mathematical in nature. This final section contains more complicated tables of data (which frequently involve Horus eye fractions), several pefsu problems which are elementary algebraic problems concerning food preparation. +

John Burnet wrote in “Early Greek Philosophy”: “The Rhind papyrus in the British Museum gives us a glimpse of arithmetic and geometry as they were understood on the banks of the Nile. It is the work of one Aahmes, and contains rules for calculations both of an arithmetical and a geometrical character. The arithmetical problems mostly concern measures of corn and fruit, and deal particularly with such questions as the division of a number of measures among a given number of persons, the number of loaves or jars of beer that certain measures will yield, and the wages due to the workmen for a certain piece of work. It corresponds exactly, in fact, to the description of Egyptian arithmetic Plato gives us in the Laws, where he tells us that children learnt along with their letters to solve problems in the distribution of apples and wreaths to greater or smaller numbers of people, the pairing of boxers and wrestlers, and so forth. This is clearly the origin of the art which the Greeks called logistikê, and they probably borrowed that from Egypt, where it was highly developed; but there is no trace of what the Greeks called arithmêtikê, the scientific study of numbers. [Source: John Burnet (1863-1928), “Early Greek Philosophy” London and Edinburgh: A. and C. Black, 1892, 3rd edition, 1920, Evansville University]

“The geometry of the Rhind papyrus is of a similar character, and Herodotus, who tells us that Egyptian geometry arose from the necessity of measuring the land afresh after the inundations, is clearly far nearer the mark than Aristotle, who says it grew out of the leisure enjoyed by the priestly caste. The rules given for calculating areas are only exact when these are rectangular. As fields are usually more or less rectangular, this would be sufficient for practical purposes. It is even assumed that a right-angled triangle can be equilateral. The rule for finding what is called the seqt of a pyramid is, however, on a rather higher level, as we should expect. It comes to this. Given the "length across the sole of the foot," that is, the diagonal of the base, and that of the piremus or "ridge," to find a number which represents the ratio between them. This is done by dividing half the diagonal of the base by the "ridge," and it is obvious that such a method might quite well be discovered empirically. It seems an anachronism to speak of elementary trigonometry in connection with a rule like this, and there is nothing to suggest that the Egyptians went any further.

Ancient Egyptian Fractions

problem from the Rhind papyrus

Mark Millmore wrote in discoveringegypt.com: “All ancient Egyptian fractions, with the exception of 2/3, are unit fractions, that is fractions with numerator 1. For example 1/2, 1/7, 1/34. Unit fractions are written additively: 1/4 1/26 means 1/4 + 1/26. and 1/4 + 1/28 = our 2/7. The hieroglyph for ‘R’ was used as the word ‘part’. In one of the ancient stories the god Seth attacked his brother the god Horus and gouged out his eye and then tore it to pieces. Fortunately for Horus the god Thoth was able to put the pieces back together and heal his eye. In honour of this story the ancient Egyptians also used the pieces of Horus’s eye to describe fractions. The right side of the eye = 1/2. The pupil = 1/4. The eyebrow = 1/8. The left side of the eye = 1/16. The curved tail = 1/32. The teardrop = 1/64. [Source: Mark Millmore, discoveringegypt.com discoveringegypt.com ^^^]

According to the website “Egyptian Fractions” put out by the University of California, Irvine: “Nowadays, we usually write non-integer numbers either as fractions (2/7) or decimals (0.285714). The floating point representation used in computers is another representation very similar to decimals. But the ancient Egyptians (as far as we can tell from the documents now surviving) used a number system based on unit fractions: fractions with one in the numerator. This idea let them represent numbers like 1/7 easily enough; other numbers such as 2/7 were represented as sums of unit fractions (e.g. 2/7 = 1/4 +1/28). Further, the same fraction could not be used twice (so 2/7 = 1/7 + 1/7 is not allowed). We call a formula representing a sum of distinct unit fractions an Egyptian fraction. [Source: Egyptian Fractions, University of California, Irvine]

“This notation is cumbersome and difficult to compute with, so the Egyptian scribes made large tables so they could look up the answers to arithmetic problems. However there is also some interesting mathematics associated with the problem of converting modern fraction notation into the Egyptian form. A number of famous mathematicians have looked at this problem, and invented different ways of doing this conversion process. Each of these methods has advantages and disadvantages in terms of the complexity of the Egyptian fraction representations it produces and in terms of the amount of time the conversion process takes. There are still some unsolved problems about whether some of these processes finish, or whether they get into an infinite loop.

Ancient Egyptian Math Puzzles

The Rhind Mathematical Papyrus is a 3,600-year-old Egyptian document with roughly 85 problems and puzzles. The brain teasers found in this document — the world’s first known ones — were practical: problems to calculate how efficient a laborer was by how many logs he carried, or to gauge the potency of beer. The very British-sounding St. Ives conundrum (the one where the seven wives each have seven sacks containing seven cats who each have seven kits, and you have to figure out how many are going to St. Ives) is found in the papyrus in an earlier form. [Source: Pam Belluck, New York Times, December 6, 2010]

Pam Belluck wrote in the New York Times, “The Rhind Mathematical Papyrus contains a puzzle of sevens that bears an uncanny likeness to the St. Ives riddle. It has mice and barley, not wives and sacks, but the gist is similar. Seven houses have seven cats that each eat seven mice that each eat seven grains of barley. Each barley grain would have produced seven hekat of grain. (A hekat was a unit of volume, roughly 1.3 gallons.)The goal: to determine how many things are described. The answer: 19,607. (The method: 7 + 7² + 7³ + 74 + 75.)

It all goes to show that making puzzles is “the most ancient of all instincts,” said Marcel Danesi, a puzzle expert and anthropology professor at the University of Toronto, who calls documents like the Rhind papyrus “the first puzzle books in history.” Dr. Danesi says people of all eras and cultures gravitate toward puzzles because puzzles have solutions. “Other philosophical puzzles of life do not,” he continued. “When you do get it you go, “Aha, there it is, damn it,” and it gives you some relief.”

But the Egyptian puzzles were not just recreational diversions seeking the comforting illusion of competence. They were serious about their mission. The Rhind papyrus’s scribe, known as Ahmes, introduced the problems by saying that he is presenting the “correct method of reckoning, for grasping the meaning of things and knowing everything that is, obscurities and all secrets.”

Ancient Egyptian Mathematical Texts

20120217-Hierogliphics Thutmose_IV_Chair_Panel_(left).jpg
Pam Belluck wrote in the New York Times The Rhind papyrus, which dates to 1650 B.C., is one of several precocious papyri and other artifacts displaying Egyptian mathematical ingenuity. There is the Moscow Mathematical Papyrus (held at the Pushkin State Museum of Fine Arts in Moscow), the Egyptian Mathematical Leather Roll (which along with the Rhind papyrus is housed at the British Museum) and the Akhmim Wooden Tablets (at the Museum of Egyptian Antiquities in Cairo). [Source: Pam Belluck, New York Times, December 6, 2010]

They include methods of measuring a ship’s mast and rudder, calculating the volume of cylinders and truncated pyramids, dividing grain quantities into fractions and verifying how much bread to exchange for beer. They even compute a circle’s area using an early approximation of pi. (They use 256/81, about 3.16, instead of pi’s value of 3.14159....)

And the documents were practical guides to navigating a maturing civilization and an expanding economy. “Egypt was going from a centralized, structured world to partially being decentralized,” Milo Gardner, an amateur decoder of Egyptian mathematical texts who has written extensively about them, told the New York Times. “They had an economic system that was run by absentee landowners and paid people in units of grain, and in order to make it fair had to have exact weights and measures. They were trying to figure out a way to evenly divide the hekat so they could use it as a unit of currency.”

So the Akhmim tablets, nearly 4,000 years old, contain lists of servants’ names, along with a series of computations concerning how a hekat of grain can be divided by 3, 7, 10, 11 and 13. The Egyptian Mathematical Leather Roll, also from about 1650 B.C., is generally considered a kind of practice test for students to learn how to convert fractions into sums of other fractions.

The Rhind papyrus contains geometry problems that compute the slopes of pyramids and the volume of various-shaped granaries. And the Moscow papyrus, from about 1850 B.C., has about 25 problems, including ways to measure ships’ parts and find the surface area of a hemisphere and the area of triangles. Especially interesting are problems that calculate how efficient a laborer was by how many logs he carried or how many sandals he could make and decorate. Or the problems that involve a pefsu, a unit measuring the strength or weakness of beer or bread based on how much grain is used to make it.One problem calculates whether it’s right to exchange 100 loaves of 20-pefsu bread for 10 jugs of 4-pefsu malt-date beer. After a series of steps, the papyrus proclaims, according to one translation: “Behold! The beer quantity is found to be correct.”

The problems in these ancient texts are not difficult by modern mathematical standards. The challenge for scholars has come in deciphering what the problems are saying and checking their accuracy. Some of the numerical equivalents are written in a symbolic system called the Eye of Horus, based on a drawing representing the eye of the sky god Horus, depicted as a falcon. Sections of the falcon’s eye are used to represent fractions: one-half, one-quarter and so on, up to one sixty-fourth.

Scholars have found a few errors in the problems, and Ahmes even wrote an incorrect number in his St. Ives problem. But over all, the equations are considered remarkably accurate. “The practical answers are solved,” Mr. Gardner said. “What is unsolved about them is the actual thinking in the scribe’s head. We don’t know exactly how he thought of it.”

Influence of Egyptian Math on the Ancient Greeks

John Burnet wrote in “Early Greek Philosophy”: “That the Greeks learnt as much from them is highly probable, though we shall see also that, from. the very first, they generalized it so as to make it of use in measuring the distances of inaccessible objects, such as ships at sea. It was probably this generalization that suggested the idea of a science of geometry, which was really the creation of the Pythagoreans, and we can see how far the Greeks soon surpassed their teachers from a remark attributed to Democritus. It runs (fr. 299) : "I have listened to many learned men, but no one has yet surpassed me in the construction of figures out of lines accompanied by demonstration, not even the Egyptian arpedonapts, as they call them." [Source: John Burnet (1863-1928), “Early Greek Philosophy” London and Edinburgh: A. and C. Black, 1892, 3rd edition, 1920, Evansville University]

“Now the word arpedovaptês is not Egyptian but Greek. It means "cord-fastener," and it is a striking coincidence that the oldest Indian geometrical treatise is called the Sulvasutras or "rules of the cord." These things point to the use of the triangle of which the sides are as 3, 4, 5, and which has always a right angle. We know that this was used from an early date among the Chinese and the Hindus, who doubtless got it from Babylon, and we shall see that Thales probably learnt the use of it in Egypt. There is no reason for supposing that any of these peoples had troubled themselves to give a theoretical demonstration of its properties, though Democritus would certainly have been able to do so. As we shall see, however, there is no real evidence that Thales had any mathematical knowledge which went beyond the Rhind papyrus, and we must conclude that mathematics in the strict sense arose in Greece after his time. It is significant in this connection that all mathematical terms are purely Greek in their origin.”

sundial

Image Sources: Wikimedia Commons, The Louvre, The British Museum, The Egyptian Museum in Cairo

Text Sources: UCLA Encyclopedia of Egyptology, escholarship.org ; Internet Ancient History Sourcebook: Egypt sourcebooks.fordham.edu ; Tour Egypt, Minnesota State University, Mankato, ethanholman.com; Mark Millmore, discoveringegypt.com discoveringegypt.com; Metropolitan Museum of Art, National Geographic, Smithsonian magazine, New York Times, Washington Post, Los Angeles Times, Discover magazine, Times of London, Natural History magazine, Archaeology magazine, The New Yorker, BBC, Encyclopædia Britannica, Time, Newsweek, Wikipedia, Reuters, Associated Press, The Guardian, AFP, Lonely Planet Guides, “World Religions” edited by Geoffrey Parrinder (Facts on File Publications, New York); “History of Warfare” by John Keegan (Vintage Books); “History of Art” by H.W. Janson Prentice Hall, Englewood Cliffs, N.J.), Compton’s Encyclopedia and various books and other publications.

Last updated September 2018